Asinh Demo

Illustration of the asinh axis scaling, which uses the transformation

\[a \rightarrow a_0 \sinh^{-1} (a / a_0)\]

For coordinate values close to zero (i.e. much smaller than the "linear width" \(a_0\)), this leaves values essentially unchanged:

\[a \rightarrow a + \mathcal{O}(a^3)\]

but for larger values (i.e. \(|a| \gg a_0\), this is asymptotically

\[a \rightarrow a_0 \, \mathrm{sgn}(a) \ln |a| + \mathcal{O}(1)\]

As with the symlog scaling, this allows one to plot quantities that cover a very wide dynamic range that includes both positive and negative values. However, symlog involves a transformation that has discontinuities in its gradient because it is built from separate linear and logarithmic transformations. The asinh scaling uses a transformation that is smooth for all (finite) values, which is both mathematically cleaner and reduces visual artifacts associated with an abrupt transition between linear and logarithmic regions of the plot.

Note

scale.AsinhScale is experimental, and the API may change.

See AsinhScale, SymmetricalLogScale.

import numpy as np
import matplotlib.pyplot as plt

# Prepare sample values for variations on y=x graph:
x = np.linspace(-3, 6, 500)

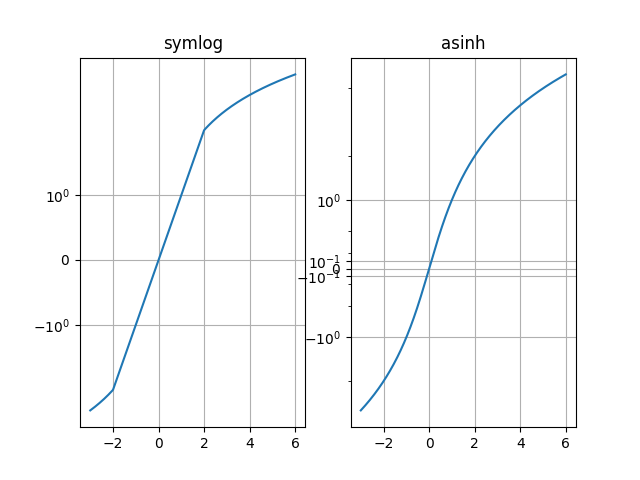
Compare "symlog" and "asinh" behaviour on sample y=x graph, where there is a discontinuous gradient in "symlog" near y=2:

fig1 = plt.figure()
ax0, ax1 = fig1.subplots(1, 2, sharex=True)

ax0.plot(x, x)
ax0.set_yscale('symlog')
ax0.grid()
ax0.set_title('symlog')

ax1.plot(x, x)
ax1.set_yscale('asinh')
ax1.grid()
ax1.set_title('asinh')

Text(0.5, 1.0, 'asinh')

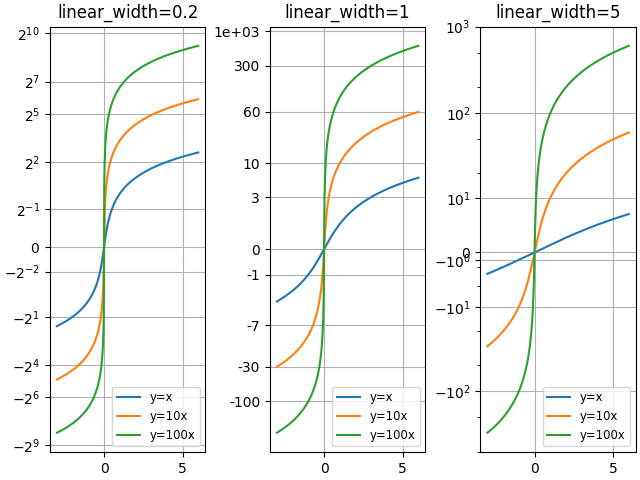
Compare "asinh" graphs with different scale parameter "linear_width":

fig2 = plt.figure(constrained_layout=True)
axs = fig2.subplots(1, 3, sharex=True)
for ax, (a0, base) in zip(axs, ((0.2, 2), (1.0, 0), (5.0, 10))):
    ax.set_title('linear_width={:.3g}'.format(a0))
    ax.plot(x, x, label='y=x')
    ax.plot(x, 10*x, label='y=10x')
    ax.plot(x, 100*x, label='y=100x')
    ax.set_yscale('asinh', linear_width=a0, base=base)
    ax.grid()
    ax.legend(loc='best', fontsize='small')

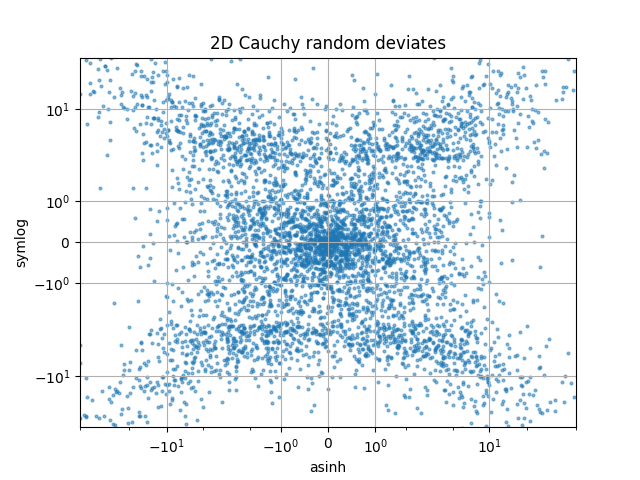
Compare "symlog" and "asinh" scalings on 2D Cauchy-distributed random numbers, where one may be able to see more subtle artifacts near y=2 due to the gradient-discontinuity in "symlog":

fig3 = plt.figure()
ax = fig3.subplots(1, 1)
r = 3 * np.tan(np.random.uniform(-np.pi / 2.02, np.pi / 2.02,
                                 size=(5000,)))
th = np.random.uniform(0, 2*np.pi, size=r.shape)

ax.scatter(r * np.cos(th), r * np.sin(th), s=4, alpha=0.5)
ax.set_xscale('asinh')
ax.set_yscale('symlog')
ax.set_xlabel('asinh')
ax.set_ylabel('symlog')
ax.set_title('2D Cauchy random deviates')
ax.set_xlim(-50, 50)
ax.set_ylim(-50, 50)
ax.grid()

plt.show()

References

• matplotlib.scale.AsinhScale

• matplotlib.ticker.AsinhLocator

• matplotlib.scale.SymmetricalLogScale