Line, Poly and RegularPoly Collection with autoscaling#

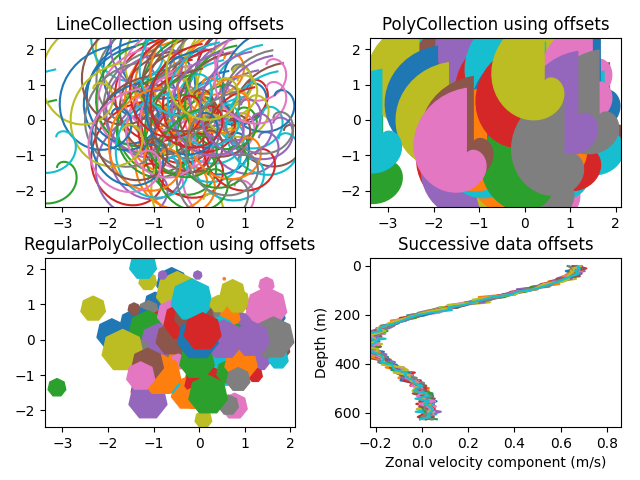
For the first two subplots, we will use spirals. Their size will be set in plot units, not data units. Their positions will be set in data units by using the offsets and offset_transform keyword arguments of the LineCollection and PolyCollection.

The third subplot will make regular polygons, with the same type of scaling and positioning as in the first two.

The last subplot illustrates the use of "offsets=(xo, yo)", that is, a single tuple instead of a list of tuples, to generate successively offset curves, with the offset given in data units. This behavior is available only for the LineCollection.

import matplotlib.pyplot as plt
from matplotlib import collections, colors, transforms
import numpy as np

nverts = 50
npts = 100

# Make some spirals
r = np.arange(nverts)
theta = np.linspace(0, 2*np.pi, nverts)
xx = r * np.sin(theta)
yy = r * np.cos(theta)
spiral = np.column_stack([xx, yy])

# Fixing random state for reproducibility
rs = np.random.RandomState(19680801)

# Make some offsets
xyo = rs.randn(npts, 2)

# Make a list of colors cycling through the default series.
colors = [colors.to_rgba(c)
          for c in plt.rcParams['axes.prop_cycle'].by_key()['color']]

fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2)
fig.subplots_adjust(top=0.92, left=0.07, right=0.97,
                    hspace=0.3, wspace=0.3)


col = collections.LineCollection(
    [spiral], offsets=xyo, offset_transform=ax1.transData)
trans = fig.dpi_scale_trans + transforms.Affine2D().scale(1.0/72.0)
col.set_transform(trans)  # the points to pixels transform
# Note: the first argument to the collection initializer
# must be a list of sequences of (x, y) tuples; we have only
# one sequence, but we still have to put it in a list.
ax1.add_collection(col, autolim=True)
# autolim=True enables autoscaling.  For collections with
# offsets like this, it is neither efficient nor accurate,
# but it is good enough to generate a plot that you can use
# as a starting point.  If you know beforehand the range of
# x and y that you want to show, it is better to set them
# explicitly, leave out the *autolim* keyword argument (or set it to False),
# and omit the 'ax1.autoscale_view()' call below.

# Make a transform for the line segments such that their size is
# given in points:
col.set_color(colors)

ax1.autoscale_view()  # See comment above, after ax1.add_collection.
ax1.set_title('LineCollection using offsets')


# The same data as above, but fill the curves.
col = collections.PolyCollection(
    [spiral], offsets=xyo, offset_transform=ax2.transData)
trans = transforms.Affine2D().scale(fig.dpi/72.0)
col.set_transform(trans)  # the points to pixels transform
ax2.add_collection(col, autolim=True)
col.set_color(colors)


ax2.autoscale_view()
ax2.set_title('PolyCollection using offsets')

# 7-sided regular polygons

col = collections.RegularPolyCollection(
    7, sizes=np.abs(xx) * 10.0, offsets=xyo, offset_transform=ax3.transData)
trans = transforms.Affine2D().scale(fig.dpi / 72.0)
col.set_transform(trans)  # the points to pixels transform
ax3.add_collection(col, autolim=True)
col.set_color(colors)
ax3.autoscale_view()
ax3.set_title('RegularPolyCollection using offsets')


# Simulate a series of ocean current profiles, successively
# offset by 0.1 m/s so that they form what is sometimes called
# a "waterfall" plot or a "stagger" plot.

nverts = 60
ncurves = 20
offs = (0.1, 0.0)

yy = np.linspace(0, 2*np.pi, nverts)
ym = np.max(yy)
xx = (0.2 + (ym - yy) / ym) ** 2 * np.cos(yy - 0.4) * 0.5
segs = []
for i in range(ncurves):
    xxx = xx + 0.02*rs.randn(nverts)
    curve = np.column_stack([xxx, yy * 100])
    segs.append(curve)

col = collections.LineCollection(segs, offsets=offs)
ax4.add_collection(col, autolim=True)
col.set_color(colors)
ax4.autoscale_view()
ax4.set_title('Successive data offsets')
ax4.set_xlabel('Zonal velocity component (m/s)')
ax4.set_ylabel('Depth (m)')
# Reverse the y-axis so depth increases downward
ax4.set_ylim(ax4.get_ylim()[::-1])


plt.show()

References

The use of the following functions, methods, classes and modules is shown in this example:

Gallery generated by Sphinx-Gallery